Bạn gặp khó khăn với các bài toán đố, chuyển động, năng suất hay lãi suất? Phương pháp giải toán bằng cách lập phương trình sẽ giúp bạn dễ dàng tìm ra đáp án! Từ bài toán đơn giản đến phức tạp – chỉ cần nắm vững cách lập phương trình, bạn sẽ chinh phục mọi thử thách! Cùng Sumenki khám phá nhé!
Các bước giải toán bằng cách lập phương trình
Bước 1: Xác định ẩn số
- Xác định đại lượng chưa biết và đặt ẩn số (thường là x).
- Xác định đơn vị tính của ẩn số.
- Nếu có điều kiện ràng buộc, cần nêu rõ điều kiện của ẩn.
Bước 2: Lập phương trình
- Biểu diễn các đại lượng khác theo ẩn số.
- Dựa vào mối quan hệ trong bài toán để lập phương trình.
Thường có các dạng quan hệ phổ biến như:
– Tổng – Hiệu: “Tổng hai số là 30”, “Số này hơn số kia 5 đơn vị”.
– Tỷ lệ: “Số này gấp 3 lần số kia”, “Hai số có tỷ số 2:3”.
– Vận tốc – Quãng đường – Thời gian: Sử dụng công thức S = v × t.
– Năng suất – Sản lượng – Thời gian: Dùng công thức S = N × T
(Sản lượng = Năng suất × Thời gian).
– Lãi suất – Tiền gửi – Tiền lãi: Dùng công thức Lãi = Vốn x Lãi suất x Thời gian
Bước 3: Giải phương trình
- Dùng các phương pháp giải phương trình để tìm ẩn số.
- Nhân, chia hai vế.
- Chuyển vế, đổi dấu.
- Quy đồng mẫu số (nếu có phân số).
Bước 4: Kiểm tra điều kiện và kết luận
- Xem kết quả tìm được có thỏa mãn bài toán không.
- Viết đáp số.
Các dạng toán thường gặp
Dạng 1: Toán về số
📌 Ví dụ: Một số tự nhiên khi gấp lên 3 lần rồi cộng thêm 7 thì được 25. Tìm số đó.
🔹 Giải:
Gọi số cần tìm là x.
Theo đề bài, ta có phương trình:
3x+7=25
Giải phương trình:
3x=25−7
3x = 18
x = 6
Kết luận: Số cần tìm là 6.
Dạng 2: Toán chuyển động (Quãng đường – Vận tốc – Thời gian)
📌 Công thức:
S = v × t
Trong đó:
S: Quãng đường
v: Vận tốc
t: Thời gian
📌 Ví dụ 2: Một người đi xe đạp từ A đến B với vận tốc 12 km/h. Sau đó, một người khác đi xe máy từ A đến B với vận tốc 36 km/h, khởi hành sau 1 giờ. Hỏi sau bao lâu người đi xe máy đuổi kịp người đi xe đạp?
Giải:
Gọi thời gian người đi xe đạp đi là x giờ.
Khi đó, quãng đường người đi xe đạp đi được: 12x km.
Thời gian người đi xe máy đi là x−1 giờ.
Quãng đường người đi xe máy đi được: 36(x−1) km.
Vì khi gặp nhau, quãng đường hai người đi bằng nhau, ta có phương trình:
12x = 36(x−1)
Giải phương trình:
12x = 36x − 36
36 = 24x
x = 1.5
🔹 Kết luận: Sau 1.5 giờ, người đi xe máy sẽ đuổi kịp người đi xe đạp.
Dạng 3: Toán làm chung – làm riêng
📌 Công thức: Nếu công việc hoàn thành trong t giờ, năng suất làm việc là 1/t.
📌 Ví dụ: Một người làm xong một công việc trong 6 giờ, người thứ hai làm xong trong 4 giờ. Hỏi nếu cả hai cùng làm thì sau bao lâu xong việc?
🔹 Giải:
- Năng suất người thứ nhất: 1/6 (công việc/giờ).
- Năng suất người thứ hai: 1/4 (công việc/giờ).
- Tổng năng suất khi làm chung:
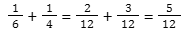
- Gọi x là thời gian hoàn thành công việc:
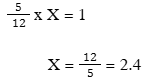
- Kết luận: Hai người làm chung sẽ hoàn thành công việc trong 2,4 giờ (2 giờ 24 phút).
Dạng 4: Toán liên quan đến hình học
📌 Ví dụ: Chu vi của một hình chữ nhật là 48 cm. Biết chiều dài gấp đôi chiều rộng. Tìm kích thước hình chữ nhật.
🔹 Giải:
- Gọi chiều rộng là x (cm), chiều dài là 2x (cm).
- Chu vi hình chữ nhật:
2(x+2x) = 48
6x = 48
x = 8
- Chiều rộng = 8 cm, chiều dài = 16 cm.
Bài tập thực hành
1. Một số tự nhiên, khi nhân với 5 rồi trừ đi 12, ta được 28. Tìm số đó.
2. Hai vòi nước chảy vào một bể, vòi thứ nhất chảy đầy bể trong 6 giờ, vòi thứ hai trong 8 giờ. Nếu mở cả hai vòi cùng lúc, sau bao lâu bể đầy?
3. Một người đi xe đạp từ A đến B trong 3 giờ, vận tốc tăng thêm 5 km/h thì chỉ mất 2 giờ. Tìm vận tốc ban đầu.
4. Một mảnh đất hình chữ nhật có chu vi 50m, biết chiều dài hơn chiều rộng 5m. Tìm kích thước mảnh đất.
Kết luận
Phương pháp lập phương trình là một công cụ mạnh mẽ để giải quyết bài toán thực tế và là nền tảng quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật. Việc rèn luyện thường xuyên sẽ giúp bạn giải toán nhanh và chính xác hơn! Cập nhật ngay những bài toán hay hơn nữa cùng với Toán – Sumenki hoặc hãy truy cập Sumenki – nền tảng học tập trực tuyến giúp bạn tiếp cận hàng trăm khóa học từ các thầy cô hàng đầu.