Tổng hợp toàn diện kiến thức về đạo hàm logarit, bao gồm nguyên lý, công thức, kỹ thuật đạo hàm hàm hợp và phương pháp logarit hóa, phục vụ học tập và nghiên cứu chuyên sâu.

🧠 PHẦN 1: KIẾN THỨC CƠ BẢN – CÔNG THỨC ĐẠO HÀM
1. Đạo hàm logarit cơ bản
– Log tự nhiên:
Ký hiệu: lnx
Miền xác định: x > 0
$$\frac{d}{dx}(\ln{x})=\frac{1}{x}\ ,\ x>0$$– Log cơ số a (a > 0, a ≠ 1):
Ký hiệu: logax với a > 0, a ≠ 1
Miền xác định: x > 0
$$\frac{d}{dx}(\log_a{x})=\frac{1}{x\ln{a}}$$🔁 PHẦN 2: ĐẠO HÀM HÀM HỢP CÓ LOGARIT
Nếu u(x) là hàm số khả vi và u(x) > 0, thì:
a. Với log tự nhiên:
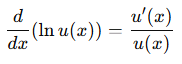
b. Với log cơ số bất kỳ:
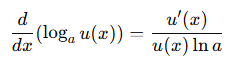
Ví dụ:
\(y=\ln{(5x^2+3x)\ =>\ y’\ =\frac{10x+3}{5x^2+3x}}\)🧮 PHẦN 3: VÍ DỤ PHÂN TÍCH TỪNG TRƯỜNG HỢP
1. Kết hợp log và nhân chia
y = ln(x2 + 1) . sinx
Dùng quy tắc đạo hàm tích:
$$y’=\frac{2x}{x^2+1}.\sin{x}+\ln{(x^2+1).\cos{x}}$$2. Kết hợp log và mũ:
y = ln(ex+1)
$$y’=\frac{e^x}{e^x+1}$$💡 PHẦN 4: LOGARIT HÓA — PHÉP ĐẠO HÀM ĐẶC BIỆT
Dùng cho các hàm dạng phức tạp như:
\(y={f(x)}^{g(x)}\)\(y=\frac{{(x^2+1)}^5}{\sqrt{(x+1){(x-1)}^3}}\)
Cách làm:
Lấy log 2 vế: \(\ln{y=\ln{\left\lceil{f(x)}^{g(x)}\right\rceil}}=g(x)\ln{f(x)}\)Đạo hàm cả hai vế theo x
Nhân lại với y để ra y′
Ví dụ:
y = xx ⇒ lny = xlnx ⇒ y′ = xx(lnx+1)
⚠️ Lưu ý quan trọng
- Chỉ lấy logarit với biểu thức dương: Hàm ln(u(x)) hay loga(u(x)) chỉ xác định khi u(x) > 0.
- Khi gặp đạo hàm của biểu thức dạng ln(f(x)), hãy dùng quy tắc đạo hàm hàm hợp.
- Nếu có tích, thương, hoặc lũy thừa, có thể sử dụng logarit hóa để đơn giản trước khi lấy đạo hàm.
🧩 PHẦN 5: CÁC VÍ DỤ NÂNG CAO
1. Biểu thức log phức hợp:
$$y=\ln{\left(\frac{x^2+3x}{x^3+1}\right)=>\ y’=\frac{\left(2x+3\right)\left(x^3+1\right)-(3x^2)(x^2+3x)}{\left(x^3+1\right)^2}}$$Hoặc dùng:
$$\ln{\left(\frac{A}{B}\right)=\ln{A}-\ln{B}=>\ y\ =\ln{(x^2+3x)-\ln{(x^3+1)=>\ y’\ =\frac{2x+3}{x^2+3x}}}}-\frac{3x^2}{x^3+1}$$📚 PHẦN 6: TỔNG HỢP CÔNG THỨC ĐẠO HÀM LOGARIT VÀ MẸO NHỚ NHANH

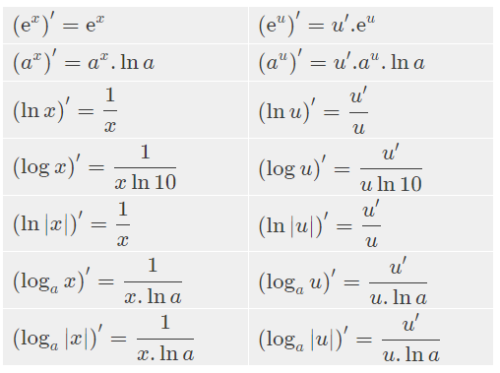
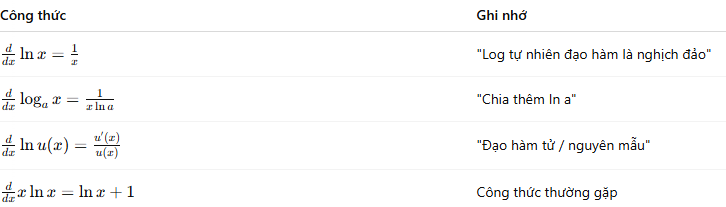
📌 Cách bấm máy tính đạo hàm logarit đơn giản nhất

🧠 PHẦN 7: BÀI TẬP TỰ LUYỆN GỢI Ý
Tính đạo hàm của các hàm sau:
y = ln(x3 + 2x + 1)
y = xx
y = log5(sinx)
\(y=\frac{\ln{(x^2+1)}}{x^3}\)Áp dụng phương pháp logarit hóa để đạo hàm:
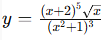
Học Toán cũng giống như xây dựng một tòa lâu đài — mỗi công thức, mỗi phương pháp là một viên gạch nền tảng.
Với hành trang kiến thức về đạo hàm logarit hôm nay, bạn đã tiến thêm một bước vững chắc trên con đường đó.
Nếu bạn mong muốn tiếp tục khám phá những kho tàng kiến thức Toán học hiện đại, hãy đồng hành cùng Sumenki — nơi học thuật được trình bày một cách dễ hiểu và gần gũi nhất!
Để tiếp tục khám phá thêm nhiều chủ đề chuyên sâu và bài tập thực hành, mời bạn ghé thăm blog toán của Sumenki.