
Có bao giờ bạn tự hỏi:
“Làm sao chỉ với vài công thức, người ta có thể tính diện tích một cánh hoa, thể tích một khối xoay, hay thời gian rơi tự do của một vật thể?”
Câu trả lời nằm ở tích phân – ngôn ngữ của sự thay đổi, của hình học vô hình, và của cả tự nhiên vận động.
Và mọi điều kỳ diệu ấy… bắt đầu từ những công thức tưởng chừng khô khan nhưng lại đầy sức mạnh.
Hãy cùng khám phá bộ công thức tích phân – như chiếc chìa khóa mở ra cả một thế giới toán học sống động.
ĐỊNH NGHĨA CƠ BẢN
1. Tích phân bất định (Indefinite Integral)
- Là phép toán ngược của đạo hàm.
- Ký hiệu: ∫f(x) dx = F(x) + C
Trong đó:
F′(x) = f(x)
C là hằng số tích phân.
2. Tích phân xác định (Definite Integral)
Đại diện cho diện tích có hướng giữa đồ thị hàm số và trục hoành.
Ký hiệu: \(\int_{a}^{b}{f(x)dx}\)Giá trị bằng F(b) − F(a), với F(x) là một nguyên hàm của f(x).
CÁC CÔNG THỨC TÍCH PHÂN CƠ BẢN
1. Tích phân cơ bản thường gặp

2. Tính chất của tích phân xác định
Tính tuyến tính: \(ab[k(x)+pg(x)]dx=kabf(x)dx+pabg(x)dx\)Đổi cận: \(\int_{a}^{b}{f(x)dx=-\int_{b}^{a}{f(x)dx}}\)
Tách khoảng: \(\int_{a}^{c}{f(x)dx=\int_{a}^{b}{f(x)dx+\int_{b}^{c}{f(x)dx}}}\)
CÁCH TÍNH TÍCH PHÂN
1. Phương pháp đổi biến số
a) Đổi biến đơn:
Dùng khi f(x) có dạng phức tạp, cần đặt u=g(x) để đơn giản biểu thức.
Công thức:
\(\int{f(g(x))g'(x)dx=\int{f(u)du}}\)b) Đổi biến lượng giác
Phổ biến với căn thức:
\(\sqrt{a^2-x^2}=>\ x=a\sin{\theta}\)\(\sqrt{a^2+x^2}=>\ x=a\tan{\theta}\)
\(\sqrt{x^2-a^2}=>\ x=a\sec{\theta}\)
2. Phương pháp từng phần (Integration by Parts)
Dùng khi tích phân của tích hai hàm.
–Công thức:
\(\int{u(x)v'(x)dx=u(x)v(x)-\int{v(x)u'(x)dx}}\)
Lưu ý: Chọn u sao cho đạo hàm đơn giản hơn, chọn v′ dễ tích phân.
Mẹo chọn u theo thứ tự: LIATE
- Logarithm: lnx
- Inverse trig: arctanx, arcsinx
- Algebraic: x,x2
- Trig: sinx, cosx
- Exponential: ex
3. Tích phân từng đoạn / hàm trị tuyệt đối
Tách đoạn theo điểm làm đổi dấu:
$$\int_{a}^{b}{\left|f(x)\right|dx=\int_{a}^{c_1}{-f(x)dx=\int_{c_1}^{c_2}{f(x)dx+…}}}$$4. Phương pháp tích phân các hàm đối xứng
Với hàm số đối xứng (chẵn hoặc lẻ):
- Nếu f(x) chẵn:
Tích phân gấp đôi phần bên phải (do tính đối xứng qua trục tung).
- Nếu f(x) lẻ:
Diện tích hai bên đối xứng nhau và triệt tiêu.
Ví dụ 1: Hàm chẵn
$$\int_{-2}^{2}{x^2dx}$$- f(x) = x2 là hàm chẵn vì f(−x) = (−x)2 = x2
- Áp dụng công thức:
Ví dụ 2: Hàm lẻ
$$\int_{-1}^{1}x^3dx$$f(x) = x3 là hàm lẻ vì f(−x) = −x3 = −f(x)
Vậy:
$$\int_{-1}^{1}x^3dx=0$$Ví dụ 3: Kết hợp
$$\int_{-1}^{1}{{(x}^3+x^2)}dx$$- x3: hàm lẻ → tích phân bằng 0
- x2: hàm chẵn → nhân đôi tích phân từ 0 đến 1
Vậy:
$$\int_{-1}^{1}{{(x}^3+x^2)}dx=\int_{-1}^{1}{x^3dx+\int_{-1}^{1}{x^2dx=0+2\int_{0}^{1}{x^2dx=2.\frac{1}{3}=\frac{2}{3}}}}$$*Chú ý:
Chỉ áp dụng được khi cận đối xứng: [−a,a]
Nếu hàm không thuần chẵn hay lẻ, có thể phân tách thành tổng hàm chẵn và hàm lẻ Ví dụ: f(x) = x3+x2 như trên
Khi hàm có chứa giá trị tuyệt đối ∣x∣, hãy xét lại tính chẵn/lẻ theo định nghĩa
5. Tích phân suy rộng (Improper Integrals)
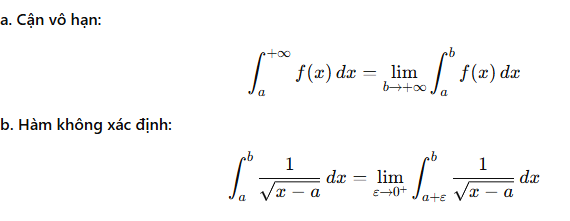
6. Phương pháp sử dụng bảng nguyên hàm
1. Mục tiêu
Dựa trên bảng các nguyên hàm thường gặp, bạn so khớp biểu thức cần tích phân với các mẫu có sẵn trong bảng để tính nhanh mà không cần chứng minh hay biến đổi phức tạp.
2. Các bước thực hiện
-Nhận diện biểu thức tích phân: So sánh hàm số với các mẫu trong bảng.
-Chuyển đổi nếu cần: Dùng đổi biến đơn giản (thường là u = ax + b) để đưa về dạng có sẵn trong bảng.
-Áp dụng công thức nguyên hàm: Tra công thức tương ứng và viết kết quả.
-Thêm hằng số tích phân (nếu là bất định) hoặc tính cận (nếu là xác định).
ỨNG DỤNG TÍCH PHÂN
1. Tính diện tích hình phẳng
a. Giữa y = f(x), trục hoành:
$$A=\ \int_{a}^{b}\left|f(x)\right|dx$$b. Giữa hai đường y = f(x), y = g(x):
$$A=\ \int_{a}^{b}\left|f(x)-g(x)\right|dx$$2. Tính thể tích vật thể tròn xoay
a. Quay quanh trục Ox:
$$V=\pi\int_{a}^{b}\left[f(x)\right]^2dx$$b. Quay quanh trục Oy:
$$V=\pi\int_{y_1}^{y_2}\left[g(y)\right]^2dy$$c. Phương pháp vỏ trụ (công thức nâng cao):
$$V=2\pi\int_{a}^{b}{x.f(x)}dx$$3. Chiều dài đường cong
Đường cong y = f(x) trên [a,b]:
$$L=\int_{a}^{b}{\sqrt{1+\left[f'(x)\right]^2}dx}$$4. Diện tích mặt tròn xoay
Đường cong y = f(x), quay quanh trục Ox:
$$S=2\pi\int_{a}^{b}{f(x).\sqrt{1+\left[f'(x)\right]^2}dx}$$MẸO HỌC TÍCH PHÂN HIỆU QUẢ
- Luôn kiểm tra xem có thể đổi biến đơn giản hay từng phần không.
- Nếu gặp f′(x), nghĩ ngay đến ln∣f(x)∣.
- Với các hàm lượng giác phức tạp, thử nhân liên hợp hoặc biến đổi lượng giác.
- Đối với tích phân xác định, chú ý đến tính chất đối xứng để rút ngắn tính toán.
CÁC DẠNG BÀI TẬP THƯỜNG GẶP
- Tính tích phân bằng phương pháp đổi biến đơn giản.
- Tính tích phân bằng phương pháp từng phần.
- Tính diện tích hình phẳng bằng tích phân.
- Tính thể tích hình tròn xoay.
- Tích phân có chứa giá trị tuyệt đối hoặc hàm nhiều đoạn.
Tổng kết:
Vậy là bạn đã đi một vòng từ công thức cơ bản đến những “chiêu độc” trong thế giới tích phân. Nếu ví giải tích là một trò chơi chiến thuật, thì các công thức tích phân chính là bộ kỹ năng đặc biệt giúp bạn “combat” mọi loại đề – từ trắc nghiệm tốc độ cho đến tự luận hóc búa.
Nhưng học công thức mà không luyện bài giống như học võ mà không tập đánh – có vũ khí mà chưa thành cao thủ! 💪
🧠 Vậy nên đừng để kiến thức ngủ yên trên giấy. Hãy: Truy cập ngay Sumenki – kho tàng kiến thức online với các giáo viên giảng dạy hàng đầu và đầy đủ bài tập, lời giải, video và mẹo xử lý thần tốc!