Hàm số bậc nhất là một trong những kiến thức quan trọng và nền tảng của toán học, đặc biệt trong lĩnh vực đại số và giải tích. Với dạng tổng quát y=ax+b (a≠0), hàm số này giúp chúng ta hiểu rõ hơn về mối quan hệ tuyến tính giữa hai đại lượng và cách biểu diễn chúng trên hệ trục tọa độ.
Định nghĩa
Hàm số bậc nhất là hàm số có dạng:
y = ax + b ( a≠0 )
Trong đó:
- a là hệ số góc (độ dốc) của đường thẳng.
- b là hệ số tự do, xác định vị trí của đường thẳng trên trục tung.
📌 Lưu ý: Hàm số bậc nhất là một hàm số đồng biến hoặc nghịch biến, không có cực trị.
Tính chất của hàm số bậc nhất
Tập xác định
Hàm số bậc nhất xác định trên tập số thực R, tức là:
D = R
Sự đồng biến, nghịch biến
- Nếu a > 0 → Hàm số đồng biến (hàm số tăng).
- Nếu a < 0 → Hàm số nghịch biến (hàm số giảm).
📌 Nhận xét:
- Nếu a > 0, khi x tăng thì y cũng tăng.
- Nếu a < 0, khi x tăng thì y giảm.
Đồ thị của hàm số bậc nhất
Đồ thị của hàm số bậc nhất y = ax + b là một đường thẳng.
Các điểm quan trọng trên đồ thị
- Giao điểm với trục tung ( tại x = 0 ):
y = b ⇒ Giao điểm: ( 0, b )
- Giao điểm với trục hoành ( tại y = 0 ):
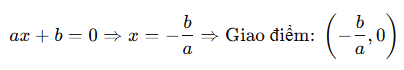
Cách vẽ đồ thị hàm số bậc nhất
Bước 1: Xác định hai điểm đặc biệt:
Bước 2: Nối hai điểm lại để tạo thành một đường thẳng.
📌 Ví dụ:
Vẽ đồ thị hàm số y = 2x − 3:
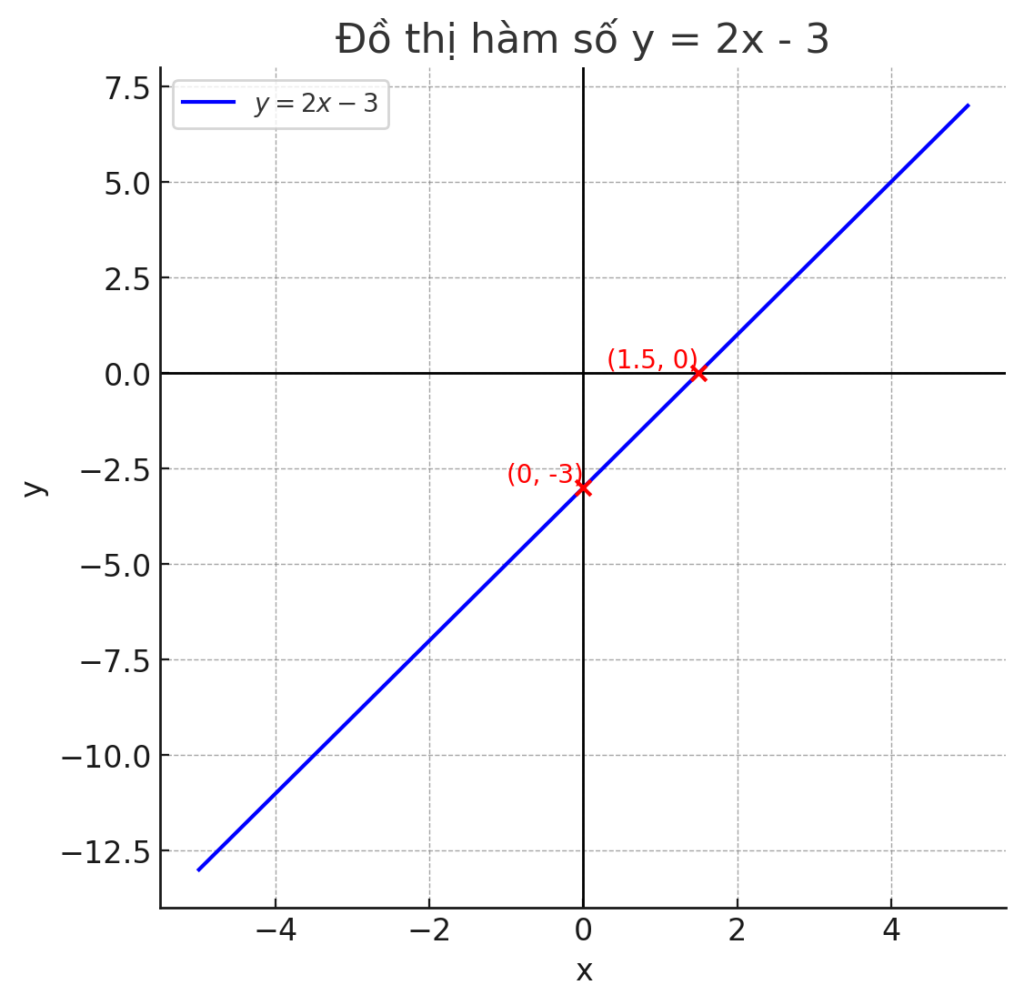
- Giao điểm với trục tung: ( 0,−3 ).
- Giao điểm với trục hoành: ( 1.5,0 ).
- Nối hai điểm để được đường thẳng.
Vị trí tương đối của hai đường thẳng
Cho hai hàm số:
y = a1x + b1, y = a2x + b2
Có ba trường hợp:
- Hai đường thẳng cắt nhau nếu a1≠a2.
- Giao điểm được tìm bằng cách giải hệ phương trình:
a1x + b1 = a2x + b2a
- Giao điểm được tìm bằng cách giải hệ phương trình:
- Hai đường thẳng song song nếu a1 = a2 nhưng b1 ≠ b2.
- Hai đường thẳng trùng nhau nếu a1 = a2 và b1 = b2.
📌 Ví dụ:
Cho hai hàm số y = 2x + 3 và y = −x + 5.
- Ta có a1 = 2, a2 = −1.
- Vì a1 ≠ a2, hai đường thẳng cắt nhau.
- Tìm giao điểm bằng cách giải phương trình:
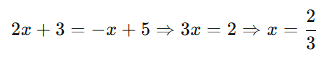
Thay vào y = 2x + 3:
Vậy giao điểm là:
Một số bài toán quan trọng
Tìm giao điểm của hai đường thẳng
- Giải hệ phương trình y1 = y2 để tìm x, rồi thay vào tìm y.
Xác định tham số để hai đường thẳng song song, trùng nhau hoặc cắt nhau
- Song song: a1 = a2, b1 ≠ b2.
- Trùng nhau: a1 = a2, b1 = b2.
- Cắt nhau: a1 ≠ a2.
Viết phương trình đường thẳng khi biết hai điểm
Muốn tìm phương trình đường thẳng đi qua hai điểm A( x1, y2 ) và B( x1, y2 ), ta dùng công thức:
📌 Ví dụ:
Tìm phương trình đường thẳng đi qua A(1,2) và B (3,6).
Hệ số góc:
Phương trình:
y − 2 = 2(x−1) ⇒ y = 2x
Vậy phương trình cần tìm là y = 2x
Ứng dụng thực tế
Kinh tế và tài chính
- Chi phí sản xuất: Nếu một doanh nghiệp có chi phí cố định là bbb và chi phí biến đổi trên mỗi đơn vị sản phẩm là aaa, tổng chi phí C(x) khi sản xuất x đơn vị sản phẩm có thể được mô tả bằng hàm số bậc nhất: C(x) = ax + b
- Doanh thu: Nếu giá bán của một sản phẩm là ppp đồng trên mỗi đơn vị, doanh thu khi bán x sản phẩm được tính bằng:
R(x) = px
Đây cũng là một hàm số bậc nhất khi p không thay đổi.
Vật lý và kỹ thuật
- Chuyển động thẳng đều: Vận tốc không đổi v của một vật chuyển động theo phương trình:
s = vt + s0
Trong đó s0 là vị trí ban đầu, s là quãng đường di chuyển được sau thời gian t.
- Sự giãn nở nhiệt: Độ dài của một vật thay đổi theo nhiệt độ theo công thức:
L = L0 +αT
Trong đó L0 là chiều dài ban đầu, α là hệ số giãn nở, và T là nhiệt độ.
Tin học và công nghệ
- Tính toán trong lập trình: Nhiều thuật toán sử dụng hàm số bậc nhất để tính toán chi phí thời gian chạy (time complexity) hoặc xác định các quy luật dữ liệu trong mô hình hồi quy tuyến tính.
- Hiệu chỉnh âm lượng hoặc ánh sáng: Trong các ứng dụng chỉnh sửa ảnh hoặc âm thanh, điều chỉnh độ sáng hoặc âm lượng có thể sử dụng các phép biến đổi tuyến tính, chẳng hạn như:
Y = aX + b
Với X là giá trị đầu vào, Y là giá trị đầu ra sau khi điều chỉnh.
Giao thông vận tải
- Quãng đường di chuyển: Một phương tiện di chuyển với tốc độ không đổi có thể tính được quãng đường đi được sau thời gian ttt theo công thức:
S = vt
- Tiền cước taxi: Một số hãng taxi tính tiền theo công thức:
P = ax + b
Với x là số km di chuyển, a là giá tiền mỗi km, và b là phí khởi hành cố định.
Môi trường và khoa học xã hội
- Mức độ ô nhiễm không khí: Nồng độ khí CO2 trong một thành phố có thể thay đổi tuyến tính theo thời gian trong một ngày nhất định, có dạng:
C = at + b
Trong đó C là nồng độ CO2, t là thời gian trong ngày.
- Dự báo dân số: Trong một số trường hợp, dân số có thể tăng trưởng theo mô hình tuyến tính:
P = P0 + rt
Với P0 là dân số ban đầu, r là tốc độ tăng dân số.
📌 Tóm tắt nhanh:
Kết luận:
Việc nắm vững hàm số bậc nhất không chỉ giúp bạn giải quyết các bài toán toán học hiệu quả mà còn là bước đệm quan trọng để tiếp cận các kiến thức nâng cao hơn như hàm số bậc hai, đạo hàm, tích phân.
Nếu bạn muốn tìm hiểu thêm về hàm số bậc nhất cũng như khám phá nhiều chủ đề môn học thú vị khác, hãy truy cập Sumenki – nơi cung cấp kiến thức rõ ràng, bài tập thực hành phong phú và phương pháp học hiệu quả giúp bạn chinh phục các môn học dễ dàng hơn bao giờ hết!