Trong toán học, bất đẳng thức không chỉ giúp ta so sánh các giá trị mà còn đóng vai trò quan trọng trong tối ưu hóa, hình học và thậm chí cả máy học! Một trong những bất đẳng thức quyền lực nhất chính là bất đẳng thức Bunhiacopxki (Cauchy-Schwarz).
Điều đặc biệt là bất đẳng thức này không chỉ có dạng tổng quát, mà còn có nhiều hệ quả mở rộng, giúp ta dễ dàng giải quyết các bài toán tối ưu và chứng minh những bất đẳng thức phức tạp hơn.

👉 Trong bài viết này, chúng ta sẽ cùng tìm hiểu:
✅ Định nghĩa & chứng minh bất đẳng thức Bunhiacopxki
✅ Hệ quả mạnh mẽ giúp mở rộng ứng dụng
✅ Ứng dụng thực tế trong toán học và khoa học dữ liệu
- Bất Đẳng Thức Bunhiacopxki Là Gì?
Bất đẳng thức Bunhiacopxki (hay còn gọi là Cauchy-Schwarz) là một trong những bất đẳng thức quan trọng nhất trong toán học, thường xuất hiện trong các bài toán về bất đẳng thức, tối ưu hóa và phân tích dữ liệu.
Công thức tổng quát của bất đẳng thức Bunhiacopxki:
📌 Dạng vectơ của bất đẳng thức này (trong không gian Euclid):
💡 Điều này có nghĩa là: Tích vô hướng của hai vectơ luôn nhỏ hơn hoặc bằng tích độ dài của chúng!
- Chứng Minh Bất Đẳng Thức Bunhiacopxki
Có nhiều cách chứng minh bất đẳng thức này, nhưng hai cách phổ biến nhất là:
Cách 1: Sử dụng phương pháp bình phương
Cách 2: Sử dụng vectơ trong không gian Euclid
Trong không gian , bất đẳng thức này có thể được suy ra từ định lý Cauchy-Schwars về tích vô hướng của hai vectơ.
- Hệ Quả Mở Rộng Của Bất Đẳng Thức Bunhiacopxki
Bất đẳng thức Bunhiacopxki không chỉ dừng lại ở dạng cơ bản mà còn có nhiều hệ quả mạnh mẽ, giúp giải quyết các bài toán tối ưu hóa, bất đẳng thức phức tạp và phân tích dữ liệu.
Hệ Quả 1: Cực Tiểu Của Tổng Bình Phương
Hệ Quả 2: Cực Đại & Cực Tiểu Của Tích Vô Hướng
Ứng dụng của hai hệ quả này:
- Giải bất đẳng thức phức tạp
- Tối ưu hóa trong phân tích dữ liệu
- Tìm cực trị trong không gian vectơ
- Ứng Dụng Của Bất Đẳng Thức Bunhiacopxki
✅ Giải toán bất đẳng thức: Chứng minh các bài toán liên quan đến bất đẳng thức Cauchy, AM-GM.
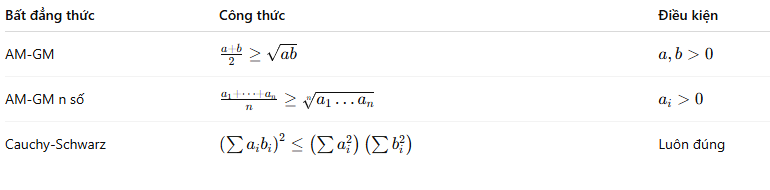
✅ Ứng dụng trong hình học: Dùng để chứng minh các bất đẳng thức trong tam giác.
1. Tính góc giữa hai vectơ
Trong không gian Euclid, nếu \(\vec{u}.\vec{v}=\left|\vec{u}\right|.\left|\vec{v}\right|\cos{\theta}\) thì BĐT CBS đảm bảo rằng: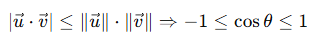
=> Cho phép xác định góc giữa hai vectơ trong không gian.
Ví dụ 3: Cho \(\vec{u}=(1,2,-1),\vec{v}=(2,0,3)\) hãy tìm góc giữa chúng.Giải:
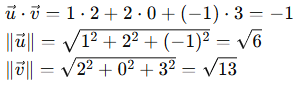
✅ Ứng dụng trong khoa học dữ liệu & AI: Dùng trong phân tích dữ liệu và tối ưu hóa thuật toán.
✅ Ứng dụng trong vật lý: Dùng để chứng minh nguyên lý bất định Heisenberg trong cơ học lượng tử.
- Bài Tập Vận Dụng
Bài 1:
Bài 2:
(Sử dụng bất đẳng thức Bunhiacopxki)
💡 Lời khuyên: Nếu chưa quen với bất đẳng thức này, bạn có thể bắt đầu bằng các dạng bài tập cơ bản hơn tại Sumenki
- Kết Luận: Bất đẳng thức Bunhiacopxki – nơi logic, vẻ đẹp và sức mạnh của Toán học hội tụ.
✅ Bất đẳng thức Bunhiacopxki là công cụ mạnh mẽ trong toán học và khoa học dữ liệu.
✅ Hệ quả của nó mở rộng ứng dụng trong tối ưu hóa và bất đẳng thức phức tạp.
✅ Hiểu rõ bất đẳng thức này sẽ giúp bạn tư duy nhanh hơn, giải quyết bài toán hiệu quả hơn!💡 Bạn đã từng áp dụng bất đẳng thức Bunhiacopxki vào bài toán nào chưa? Hãy chia sẻ với chúng mình nhé! 🚀